Voyage dans les réseaux neuronaux (1ère partie) : les neurones artificiels
sur
L'intelligence artificielle (IA) et l'apprentissage automatique (ML) sont deux des sujets les plus brûlants de l'industrie électronique et informatique. Grâce aux succès de l'IA qui font la une des médias, lorsqu'elle réussit à battre les meilleurs joueurs de Go du monde [1], ou en dépit de ses échecs, avec les accidents de véhicules sans conducteurs [2], l'intelligence artificielle fait désormais partie de notre univers quotidien. Si le ML et l'IA se sont démocratisés grâce à des outils fonctionnant dans le nuage comme TensorFlow, ces plateformes aussi énormes que puissantes peuvent sembler intangibles si vous essayez de comprendre comment cela fonctionne de manière très pratique. Dans cette série consacrée aux réseaux neuronaux, nous revenons à l'essentiel en explorant la plupart des éléments de base de ces systèmes. Au fur et à mesure de notre progression, vous trouverez de nombreux exemples à essayer, des projets de ML parfois sympas, parfois obscurs, et à la fin nous doterons même un Arduino d'un cerveau. Plongeons maintenant dans le sujet passionnant des réseaux neuronaux.
Défis informatiques
L'IA et le ML sont « les » défis informatiques de notre époque. L'IA a pour finalité d'utiliser des ordinateurs pour imiter l'intelligence humaine. Le ML sert, pour sa part, à reconnaître des formes ou des modèles constitués de données structurées et semi-structurées. L'un et l'autre nécessitent des investissements annuels importants dans des projets de recherche et des développements technologiques de semi-conducteurs et de plateformes informatiques. Et, grâce au « nuage », la technologie est facilement accessible à ceux qui veulent explorer et tester leurs idées.
Mais en quoi consistent les réseaux neuronaux ? Comment fonctionnent tous ces algorithmes intelligents ? Comment apprennent-ils ? Quelles sont leurs limites ? Et est-il possible de s'amuser avec les rouages du ML sans s'inscrire à un énième service en nuage ? Ce sont précisément ces questions que cette courte série sur les réseaux neuronaux va aborder, en quatre parties :
- 1ère partie — Les neurones artificiels : dans cette partie de la série sur les réseaux neuronaux, nous commençons par remonter aux années 1950 pour examiner les premières recherches destinées à développer un neurone artificiel. De là, nous allons passer rapidement à la mise en œuvre d'un logiciel de perceptron multicouche (MLP) qui utilise la rétropropagation pour « apprendre ».
- 2e partie — Les neurones logiques : l'un des défis des premiers neurones était leur incapacité à résoudre la fonction XOR (OU exclusif). Nous allons examiner si notre MLP peut résoudre ce problème et visualiser comment le neurone apprend.
- 3e partie — Les neurones pratiques : nous allons appliquer notre MLP à une partie du problème de la conduite autonome. Il s'agira de reconnaître l'état des feux de signalisation à l'aide d'un programme sur PC.
- 4e partie — Les neurones embarqués : nous terminons cette série en nous focalisant sur ce type de neurone. Si cela fonctionne sur un PC, cela devrait fonctionner sur un microcontrôleur, non ? Grâce à un Arduino et à un capteur RVB, nous allons détecter à nouveau les couleurs des feux de signalisation.
Un apprentissage nonchalant
Si l'apprentissage est difficile pour les humains, il semble l'être aussi pour l'IA. Dans le cadre de recherches menées par l'université technique de Berlin, l'Institut Fraunhofer pour les télécommunications et l'université de technologie et de design de Singapour (SUTD), les systèmes d'IA ont dû justifier leurs stratégies de prise de décision [13]. Les résultats ont été révélateurs. Si les systèmes d'intelligence artificielle ont tous accompli leur tâche de manière admirable, ils ont fait preuve d'un culot époustouflant dans leur prise de décision. Ainsi, un algorithme a correctement déterminé la présence d'un navire sur une image, mais en fondant sa décision sur le fait que de l'eau apparaissait sur la photo. Un autre a détecté à juste titre que les images contenaient des chevaux à partir de la présence d'une indication de copyright, et non grâce aux caractéristiques visuelles de l'animal.
Réseaux neuronaux : un peu d'histoire à propos des neurones
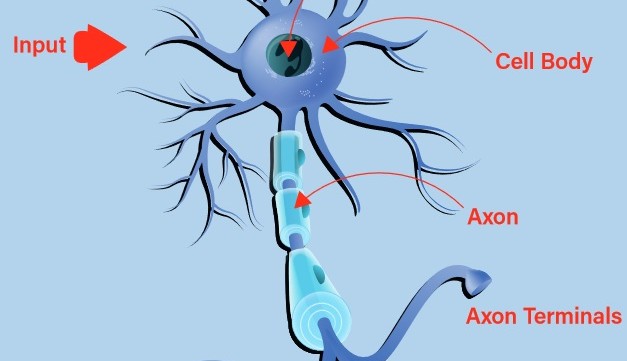
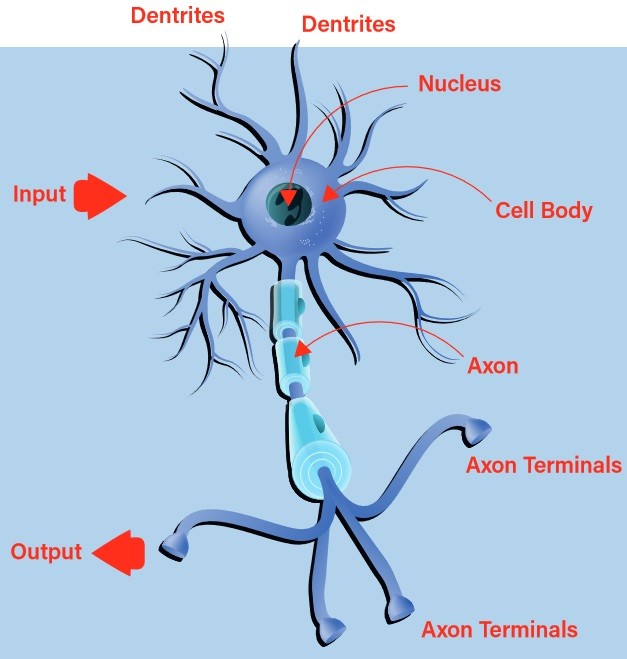
Les premières tentatives de création d'un neurone digital ou artificiel se sont inspirées de la nature. Un neurone biologique reçoit des entrées par ses dendrites et transmet la sortie résultante par son axone vers les terminaisons axonales (figure 1). La décision d'émettre ou non un stimulus en sortie, connue sous le nom de décharge du neurone, est prise par un processus appelé « activation ». Si les entrées sont conformes à un modèle appris, le neurone s'active. Dans le cas contraire, il ne le fait pas. On peut rapidement constater qu'avec des chaînes de neurones biologiques interconnectés, il est possible de reconnaître des modèles très complexes.
Les premiers neurones artificiels mis au point étaient des réseaux McCulloch-Pitts, également connus sous le nom d'unités logiques de seuil (TLU). Il s'agissait de simples « machines décisionnelles » capables de reproduire les fonctions de portes logiques. Elles n'acceptaient et ne produisaient que des valeurs logiques 0 et 1. Pour mettre en œuvre leurs capacités de reconnaissance de formes, des valeurs de pondération devaient être déterminées mathématiquement ou heuristiquement pour chaque entrée. Parfois, une entrée supplémentaire était également nécessaire (figure 2, fonctions ET et OU).
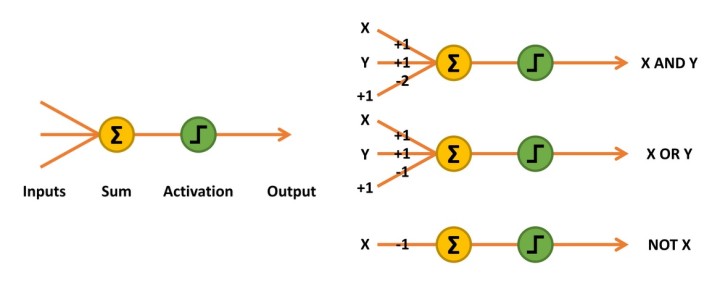
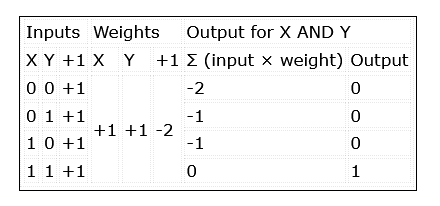
Figure 2 : Un réseau McCulloch-Pitts additionne les entrées multipliées par leurs poids, en activant une sortie 1 si le résultat est égal ou supérieur à 0.
Les entrées du réseau sont simplement multipliées par leurs poids et additionnées. La décision de produire un 1 en sortie, ou d'activer le neurone, est mise en œuvre à l'aide d'une unité de seuil linéaire. Si le résultat est égal ou supérieur à 0, un 1 est émis. Sinon, la sortie est 0 (tableau 1).
Perceptrons
L'étape suivante du développement a eu lieu dans les années 1950 avec les travaux du psychologue Frank Rosenblatt [3]. Son perceptron conservait les entrées binaires et la prise de décision par l'unité de seuil linéaire de la TLU McCulloch-Pitts. La sortie était également une valeur binaire 0 ou 1. Ce perceptron se distinguait cependant de deux manières : le niveau de seuil (appelé thêta, Θ) pour décider de la valeur de sortie était ajustable, et il acceptait une forme limitée d'apprentissage (figure 3).
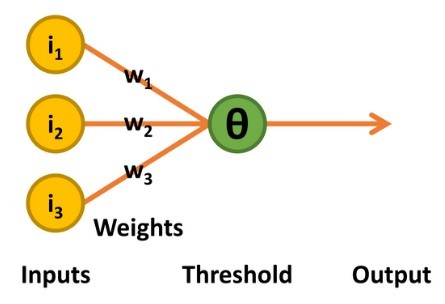
Le processus d'apprentissage fonctionne de la manière suivante : le perceptron ne produit une valeur 1 que si la somme du produit des entrées et des poids est supérieure à Θ. Si la sortie par rapport à la combinaison des entrées est correcte, rien n'est modifié.
Si une valeur 1 est produite alors qu'un 0 est requis, le niveau de seuil Θ est augmenté de 1. De plus, tous les poids associés aux entrées 1 sont réduits de 1. Si l'inverse se produit, c'est-à-dire si une valeur 0 est émise alors qu'un 1 est requis, tous les poids associés aux entrées 1 sont augmentés de 1.
Le raisonnement qui sous-tend ce processus est que seules les entrées ayant une valeur 1 peuvent contribuer à une sortie non désirée 1. Il est donc logique de réduire leur impact en diminuant les poids correspondants. Inversement, seules les entrées ayant une valeur 1 peuvent contribuer à la sortie 1 souhaitée. Si la sortie est 0, et non 1 comme souhaité, les poids associés doivent être augmentés.
En 1958, le « perceptron Mark I » a été construit sous la forme d'un dispositif matériel, après avoir été implémenté à l'aide d'un logiciel sur un IBM 704 [4]. Connecté à 400 cellules photoélectriques au sulfure de cadmium formant une caméra rudimentaire et utilisant des moteurs connectés à des potentiomètres pour mettre à jour les poids pendant l'apprentissage, il pouvait, une fois entraîné, reconnaître la forme « triangle » [5].
Le problème des perceptrons
Bien que la démarche ait ouvert une nouvelle ère où un système électronique pouvait potentiellement apprendre, un problème essentiel se posait : le dispositif ne pouvait résoudre que des problèmes linéairement séparables. Pour en revenir à l'ancienne TLU McCulloch-Pitts, les fonctions simples ET, OU, NON, NON ET et NON OU sont toutes linéairement séparables. Cela signifie qu'une seule ligne peut séparer les sorties souhaitées (par rapport aux entrées) des sorties non souhaitées (figure 4). Les fonctions OU exclusif (et la fonction complémentaire NON OU exclusif) sont différentes. Lorsque les entrées sont identiques (00 ou 11), la sortie est 0, mais lorsque les entrées sont différentes (01 ou 10), la sortie est 1. Il faut donc que la sortie souhaitée soit classée dans un groupe par rapport aux entrées. En d'autres termes, le perceptron ne peut pas être entraîné à apprendre comment fonctionne un OU exclusif ou un NON OU exclusif ou à reproduire sa fonction.
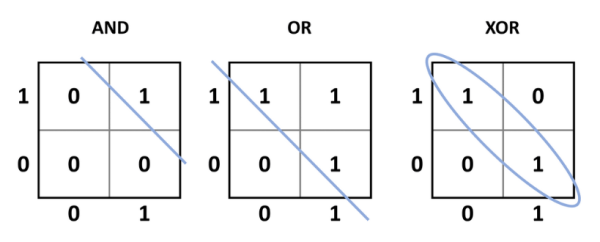
être séparées linéairement, à l'aide d'une ligne droite, des états de sortie 0. Pour le OU exclusif, les états de sortie 1
ne peuvent pas être séparés linéairement des états de sortie 0. C'est quelque chose qu'un perceptron ne peut pas apprendre.
L'autre problème essentiel réside dans la fonction d'activation utilisée. L'unité de seuil linéaire pouvait effectuer un saut brusque entre l'état inactif et l'état actif. Les recherches qui ont abouti au réseau de type règle delta [6] ont montré que la descente de gradient était un élément crucial du processus d'apprentissage des réseaux neuronaux. Cela signifiait également que toute fonction d'activation devait être différentiable. Le saut brusque de 0 à 1 dans l'unité de seuil linéaire n'est pas différentiable au point de transition (la pente devient infinie), et le reste de la fonction délivre simplement l'état 0 (la sortie reste inchangée).
Il a été proposé qu'un réseau multicouche comportant un ou plusieurs nœuds cachés entre les nœuds d'entrée et de sortie permettrait de résoudre le problème du OU exclusif. De plus, une fonction différentiable, telle que la fonction logistique (figure 5), une courbe sigmoïde, pourrait constituer une fonction d'activation progressive acceptant l'apprentissage par descente de gradient. Le principal problème résidait dans l'apprentissage : comment effectuer l'entraînement pour tous les poids ?
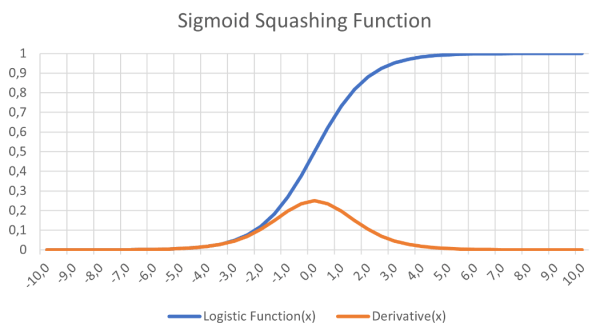
l'apprentissage par descente de gradient dans les réseaux neuronaux.
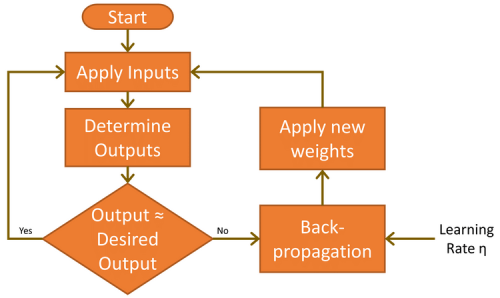
L'approche de la règle delta avait montré qu'en calculant l'erreur quadratique du réseau (sortie souhaitée – sortie réelle) et en mettant en œuvre un taux d'apprentissage, les poids du réseau pouvaient être successivement améliorés jusqu'à ce que l'ensemble optimal de vecteurs de poids ait été trouvé (figure 6). L'ajout d'une couche de nœuds cachés entre l'entrée et la sortie a rendu le calcul plus compliqué, mais pas impossible, comme nous allons le voir.
deux nœuds de sortie. Les nœuds cachés et de sortie peuvent utiliser une courbe sigmoïde pour
déterminer leur sortie au cours de la phase de propagation avant.
Perceptron multicouche
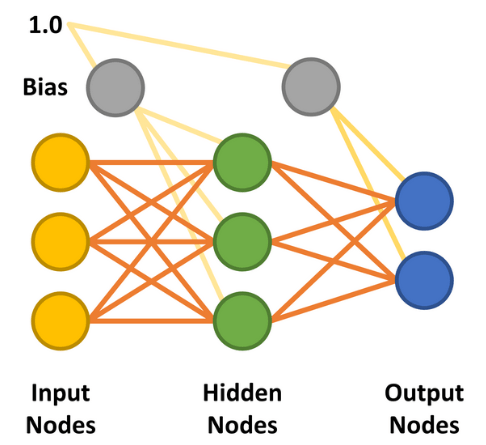
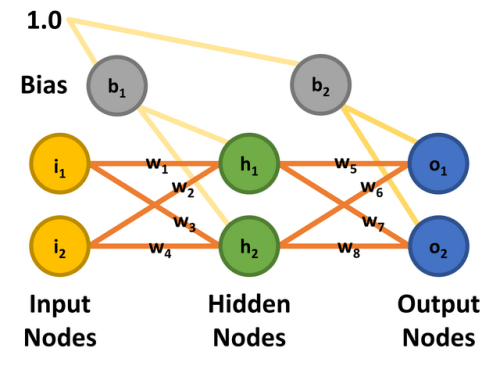
C'est l'ajout de la couche cachée qui a permis de créer le perceptron multicouche (MLP). La forme la plus simple de réseau neuronal MLP utilise une seule couche cachée. Tous les nœuds sont reliés (autrement dit « entièrement connectés ») et des poids sont attribués entre chaque nœud d'entrée et chaque nœud caché, ainsi qu'entre chaque nœud caché et chaque nœud de sortie (figure 7). Les lignes entre les nœuds représentent les poids. Les entrées souhaitées sont appliquées aux nœuds d'entrée (valeurs comprises entre 0,0 et 1,0), et le réseau calcule la réponse de chaque nœud caché et de chaque nœud de sortie - une étape connue sous le nom de phase de propagation avant. Le résultat obtenu doit indiquer que les valeurs d'entrée correspondent à une catégorie de sortie que le réseau a apprise.
À titre d'exemple, les entrées pourraient être liées à une caméra de 28 × 28 pixels pointée sur des chiffres manuscrits. La base de données MNIST de chiffres manuscrits contenant uniquement ces tailles d'images pourrait constituer l'ensemble d'apprentissage [7]. Chacune des sorties représenterait l'un des chiffres de 0 à 9. Le chiffre 7 étant tenu devant la caméra, chaque sortie indiquerait la probabilité que l'entrée ait cette valeur. La sortie 0 indiquera, avec un peu de chance, qu'il est peu probable que le chiffre écrit à la main soit un 0, tout comme les huit autres sorties. Mais la sortie 7 devrait indiquer une forte probabilité que le nombre manuscrit soit un 7. Après entraînement, cette sortie devrait fonctionner comme prévu pour un 7 provenant des données d'entraînement ou écrit à la main et reconnaissable par un humain.
Avant cela, le réseau doit apprendre la tâche à accomplir. Pour ce faire, on applique l'entrée (des 7 écrits à la main) et on analyse les résultats fournis par les sorties. Comme il est peu probable qu'ils soient corrects dès la phase initiale, un cycle d'apprentissage est exécuté pour modifier les poids afin de réduire l'erreur. Ce processus itératif, appelé rétropropagation, est exécuté plusieurs milliers de fois jusqu'à ce que la précision du réseau réponde aux exigences de l'application. Dans l'univers de l'apprentissage automatique (ML), ce processus est appelé « apprentissage supervisé ».
Il existe deux autres facteurs importants à prendre en compte durant les phases de propagation avant et de rétropropagation. Le premier est le phénomène du biais. Une valeur de biais de 1,0 multipliée par un poids (entre 0,0 et 1,0) est appliquée aux nœuds des couches cachées et de sortie pendant la phase de propagation avant. Son rôle est d'améliorer la capacité du réseau à résoudre les problèmes et, en substance, de solliciter la fonction d'activation logistique (voir figure 5) vers la gauche ou la droite. L'autre valeur est le taux d'apprentissage, là encore une valeur comprise entre 0,0 et 1,0. Comme son nom l'indique, cette valeur détermine la vitesse à laquelle le MLP apprend à résoudre le problème donné. Elle est également appelée « vitesse de convergence ». Trop basse, le réseau risque de ne jamais résoudre le problème avec un niveau de précision suffisant. Et si elle est trop élevée, le réseau risque d'osciller pendant l'apprentissage et de ne pas donner un résultat suffisamment précis (voir également le paragraphe « Limites de l'apprentissage par gradient »).
Le MLP décrit ici pourrait être considéré comme une version standard. Mais la mise en œuvre des réseaux neuronaux est possible de multiples façons. Ils peuvent notamment posséder plusieurs couches cachées, ne pas connecter complètement les nœuds, relier les nœuds ultérieurs aux nœuds antérieurs et utiliser différentes fonctions d'activation [8].
Réseaux neuronaux : limites de l'apprentissage par gradient
Il arrive qu'un réseau neuronal soit apparemment incapable d'apprendre, bien qu'il ait précédemment assimilé la fonctionnalité requise avec la même configuration de nœuds. Cette situation peut être due au fait que le réseau reste bloqué dans un « minimum local » au lieu de trouver un « minimum global » de la fonction d'erreur.
Le perceptron multicouche (MLP) en action
Le principe étant clair, nous l'espérons, nous allons maintenant examiner un exemple concret. Il fait suite à un excellent article de Matt Mazur, qui a pris le temps d'expliquer la rétropropagation dans un MLP à une seule couche masquée [9]. L'analyse menée ici sera à un niveau élargi, mais les personnes intéressées (et qui n'ont pas peur des mathématiques) peuvent étudier l'article de Matt pour plus de détails. Une fois le principe mathématique de fonctionnement abordé, nous allons examiner la mise en œuvre du MLP sous forme de logiciel, avec les mêmes paramètres que ceux utilisés pour cette analyse théorique. Si vous souhaitez aller plus loin, il existe une feuille de calcul Excel qui correspond à l'exemple traité par Matt. Il suffit de télécharger ou de cloner le référentiel GitHub [10] et d'ouvrir le fichier workedexample/Matt Mazur Example.xlsx dans le dossier.
Pour simplifier les choses, nous utilisons un MLP à deux entrées et deux sorties avec deux nœuds masqués. Les nœuds d'entrée sont libellés i1 et i2, les nœuds cachés h1 et h2 et les nœuds de sortie o1 et o2. Pour cet exercice, l'objectif est d'entraîner le réseau à produire 0,01 sur le nœud o1 et 0,99 sur o2 lorsque le nœud i1 est à 0,05 et i2 est à 0,10. Il y a huit poids (w1 à w8) et deux valeurs de biais (b1 et b2). Pour que les calculs puissent être reproduits, tous les nœuds d'entrée, les biais et les poids se voient attribuer les valeurs indiquées à la figure 8 et correspondent à l'article de Matt Mazur.
Propagation avant
La phase de propagation avant pour calculer les sorties o1 et o2 fonctionne comme suit. Chaque nœud caché reçoit une entrée qui est la somme nette des entrées multipliées par les poids, plus l'entrée de biais (b1 = 0,35). En utilisant le processus et les équations fournis par Matt Mazur, l'entrée de h1 est la somme de i1 multipliée par w1 (0,15), i2 multipliée par w2 (0,20) et b1 (0,35).
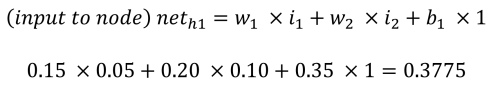
La valeur de sortie de chaque nœud caché est déterminée par la fonction (d'activation) logistique, qui écrase la sortie du nœud caché entre 0,0 et 1,0. Cette valeur est calculée comme suit :
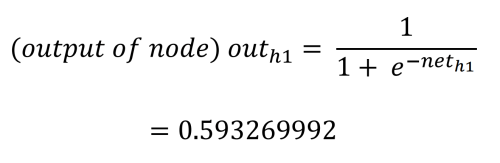
En répétant le processus pour h2 (avec w3 = 0,25, w4 = 0,3 et b1 = 0,35), on obtient :
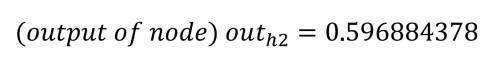
Les entrées nettes des nœuds de sortie sont calculées de la même manière, en utilisant les valeurs de sortie calculées des nœuds cachés et en appliquant les poids 5 à 8 (w5 = 0,4, w6 = 0,45, w7 = 0,5 et w8 = 0,55) et la valeur du biais b2 = 0,60.
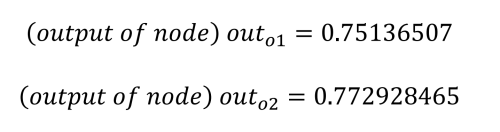
Comme nous l'avons déjà dit, notre objectif est d'obtenir une sortie de 0,01 pour o1 et de 0,99 pour o2, mais nous pouvons constater que nous sommes assez loin de ce résultat. L'étape suivante consiste à calculer l'erreur de chaque sortie en utilisant la fonction d'erreur quadratique, ainsi que l'erreur totale, comme suit :
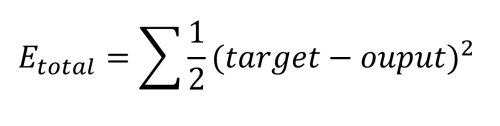
Celle-ci est calculée pour chaque sortie comme suit :
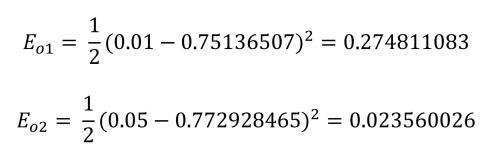
Enfin, l'erreur totale du réseau peut être établie :
L'étape suivante consiste à déterminer comment améliorer cette erreur.
Rétropropagation
La rétropropagation constitue le cœur de l'apprentissage. Le processus consiste ici à déterminer la contribution de chaque poids à l'erreur totale. Il commence par examiner les poids entre les nœuds cachés et les nœuds de sortie. Ce qui complique les choses, c'est que w5 contribue à l'erreur totale par le biais de deux nœuds de sortie, o1 et o2, qui sont également influencés par les poids w6 à w8. Il convient également de noter que les valeurs de biais ne jouent aucun rôle dans ces calculs
Les mathématiques requises pour définir ceci sont assez complexes, mais elles se limitent à quelques simples opérations de multiplication, d'addition et de soustraction. Le calcul de la nouvelle valeur de w5 en tenant compte du taux d'apprentissage choisi, η (0,5), s'effectue comme suit :
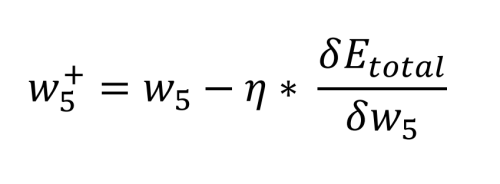
À partir de là, nous pouvons revoir les anciens poids et les comparer avec les nouveaux poids pour w5 à w8 :

En effectuant un rapide contrôle de vraisemblance, nous pouvons constater que cela fonctionne. Nous voulons que o1 soit diminué par w5 et w6 vers 0,01, et que o2 soit augmenté vers 0,99 par w7 et w8.
L'étape finale consiste à déterminer la contribution sur l'erreur en sortie des poids entre les entrées et les nœuds cachés. Comme précédemment, les mathématiques se réduisent à de simples opérations de multiplication, d'addition et de soustraction. En fait, l'équation est la même que celle utilisée pour calculer les nouveaux poids w5 à w8. Ce qui est différent, c'est la façon dont est calculée l'erreur totale par rapport au poids (initialement w1), car la sortie de la couche cachée dépend d'une autre entrée et d'un autre poids (pour h1, i1 et w1 ainsi que i2 et w2) :
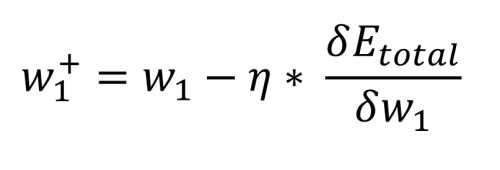
Encore une fois, la valeur de biais ne joue aucun rôle dans ce calcul. Nous pouvons maintenant comparer les anciens poids w1 à w4 et les nouveaux :

Une fois les nouveaux poids déterminés, il est possible de remplacer les anciens par les nouveaux et d'effectuer une nouvelle phase vers l'avant. Tant que l'erreur de sortie reste supérieure à la valeur souhaitée, les phases de rétropropagation peuvent être répétées comme décrit ici.
Mise en œuvre du MLP dans l'environnement Processing
Pour démontrer ce réseau neuronal simple, il a été codé de A à Z sous la forme d'une classe utilisable dans Processing [11], l'environnement de développement conçu pour promouvoir le codage dans les arts visuels. Les capacités visuelles de l'IDE permettent d'afficher aisément des graphiques 2D et 3D. Une console de sortie texte permet également de tester les idées rapidement et facilement. Le code ci-après figure dans le référentiel mentionné [10].
Le code pour mettre en œuvre le MLP se trouve dans le dossier processing/neural/neural.pde. Il suffit d'ajouter ce fichier à tout projet Processing qui doit l'utiliser. La classe Neural peut être instanciée pour prendre en charge un nombre quelconque de nœuds d'entrée, cachés et de sortie. Pour reproduire l'exemple déjà traité, le fichier processing/nn_test/nn_test.pde doit être ouvert dans Processing.
La création d'un réseau neuronal est assez simple. Tout d'abord, le constructeur de classe Neural (dans nn_test.pde) est appelé pour créer un objet, appelé ici network, en définissant le nombre souhaité d'entrées, de nœuds cachés et de sorties (2, 2 et 2). Une fois l'objet créé, d'autres fonctions membres sont appelées pour définir le taux d'apprentissage et les biais des nœuds cachés et des nœuds de sortie, comme dans l'exemple de croquis.
Le constructeur initialise également les poids avec des valeurs aléatoires comprises entre 0,25 et 0,75. Pour correspondre à l'exemple, nous modifions les poids comme indiqué dans le listage 1 où les valeurs d'entrée et les valeurs de sortie souhaitées sont également définies.

L'exemple de code active également un mode « verbeux » qui permet d'afficher le travail pour chaque étape des calculs. Ceux-ci doivent correspondre aux résultats affichés dans la feuille de calcul Excel.
Après activation de Run d'un simple clic dans Processing, la console en mode texte doit afficher le résultat suivant :
...forwardpass complete. Results:
For i1 = 0.05 and i2 = 0.1
o1 = 0.75136507 (but we want: 0.01 )
o2 = 0.7729285 (but we want: 0.99 )
Total network error is: 0.2983711
Après cela, l'apprentissage est activé et une phase vers l'avant est à nouveau exécutée, suivie de l'étape de rétropropagation. En résulte la sortie des poids nouveaux et anciens et le calcul d'une nouvelle phase vers l'avant pour déterminer les nouvelles valeurs et erreurs des nœuds de sortie :
New Hidden-To-Output Weight [ 0 ][ 0 ] = 0.3589165, Old Weight = 0.4
New Hidden-To-Output Weight [ 1 ][ 0 ] = 0.40866616, Old Weight = 0.45
New Hidden-To-Output Weight [ 0 ][ 1 ] = 0.5113013, Old Weight = 0.5
New Hidden-To-Output Weight [ 1 ][ 1 ] = 0.56137013, Old Weight = 0.55
New Input-To-Hidden Weight[ 0 ][ 0 ] = 0.14978072, Old Weight = 0.15
New Input-To-Hidden Weight[ 1 ][ 0 ] = 0.19956143, Old Weight = 0.2
New Input-To-Hidden Weight[ 0 ][ 1 ] = 0.24975115, Old Weight = 0.25
New Input-To-Hidden Weight[ 1 ][ 1 ] = 0.2995023, Old Weight = 0.3
Nous pouvons voir que les valeurs représentent les poids 5 à 8, puis 1 à 4. Elles correspondent également aux calculs effectués à la main précédemment (à quelques petites exceptions près dues à des erreurs d'arrondi).
Que faire ensuite avec le MLP et les réseaux neuronaux ?
Vous avez envie d'en savoir plus sur les réseaux neuronaux ? Maintenant que vous comprenez bien le fonctionnement d'un réseau neuronal MLP et de l'exemple de classe Neural fourni ici pour Processing, vous êtes en position idéale pour entreprendre d'autres expériences en toute indépendance. Voici quelques suggestions :
- Exécuter l'apprentissage en boucle — Combien de périodes sont-elles nécessaires pour obtenir une erreur de réseau de 0,001, 0,0005 ou 0,0001 ?
- Commencer avec différents biais et poids — Quel est l'impact sur le nombre de périodes nécessaires à l'apprentissage ? Le réseau neuronal échoue-t-il parfois dans un apprentissage ?
- Mettre les sorties en correspondance avec les entrées — Essayez de générer un graphique 3D de chaque sortie par rapport aux entrées une fois que le réseau a appris ce qu'il a à faire. Le résultat est-il conforme à vos attentes ? Peut-être préfèrerez-vous essayer Chart-Studio de Plotly plutôt que d'utiliser une feuille de calcul [12] pour tracer les données de sortie.
Dans le prochain article de cette série, nous apprendrons à notre réseau neuronal à mettre en œuvre des portes logiques et à visualiser son processus d'apprentissage.
Vous avez des questions ou des commentaires concernant les réseaux neuronaux ou tout autre sujet abordé dans cet article ? Envoyez un courrier électronique à l'auteur à l'adresse stuart.cording@elektor.com.
Traduction: Pascal Godart


Discussion (0 commentaire(s))